Introduction
Before machine learning became polular,numerous attempts were done to research face recognition. One of the successful attempts is eigenface for recognition, which utlizes a kind of linear algebra technique called Principal Component Analysis (PCA). Although the original paper “eigenface for recognition” was published in 1991, and now the results of machine learning are much ahead of PCA, it still metrits study. There is a great deal of useful study material available online, so I will not elaborate on PCA and eigenface here.
The purpose of this post is to introduce the PCA-based facial recognition implementation in C++ from scratch. This application has three main functions: collecting face images for training, training an eigenface recognizer, and performing face recognition in real time.
Steps to Implement PCA
Assume, there are 100 face images prepared for training, resolution is 100x100.
- Represent every face image (100x100) as row vector $I$ (10000x1)
- Put 100 faces row vector $I$ (10000x1) to one matrix $L$ (10000x100), each column represents one face
- Compute the average face vector $W$ (10000x1) of above 100 faces row vector
- Subtract average face $W$ (10000x1) from each column of matrix $L$ (10000x100), to get a new matrix $O$ (10000x100)
- Compute covariance matrix $C$ (10000x10000): $C = O O^T$
- Compute the eigenvectors $u_i$ of $C$
- Normalize each eigenvector $|u_i|=1$
- Keep $K$ largest eigenvectors
- Get all characteristic faces ($Z_1, Z_2 …, Z_{100}$) by multiplying eigenvector and (each original face row vector $I$ – average face $W$), then save all characteristic faces in the database.
Note: In step 6, because matrix $C$ is 10000x10000, it’s very large and need a lot of computation power to get eigenvector. When I use eigen function of OpenCV to calculate eigenvector of covariance matrix $C$, there is only one non-zero number for each eigenvector(10000x1), it’s not accurate result. (I use OpenCV 3.1.0 here to do some basic image processing.)
So we construct another covariance matrix $D$ (100x100): $D = O^TO$, then compute the eigenvector $v_i$ of $D$.
Prove:
$Dv_i = u_iv_i$
$O^TOv_i = u_iv_i$
$OO^TOv_i = u_iOv_i$
$u_i = Ov_i$
So lastly we can get eigenvector $u_i$ by multiplying matrix $O$ and $v_i$, this result is more accurate.
Steps of Face Recognition
- Represent each input test face as row vector $A$
- Subtract average face $W$ from input row vector $A$, to get a new vector $B$
- Project the row vector $B$ into eigenspace by multiplying eigenvector $u_i$ and $B$, to get a characteristic face vector $Y$
- Compute Euclidean distance between $Y$ and ($Z_1, Z_2 …, Z_{100}$), find the smallest one.
The program keeps largest 100 eigenvectors to use in recognition.
For unknown faces, when the program computes Euclidean distance, if the smallest distance is larger than a threshold we defined, the program will recognize it as “unknown face”.
To reject sudden disturbance of wrong recognition, the program only returns result when it recognizes same face from more than 5 out of 8 continuous input faces, frame capture rate of webcam is high enough (>30fps).
Peoject Code Structure
You can click here to get the full code, it has detailed explanation. The PCA process was implemented according to the original paper, not call PCA functuon of OpenCV.
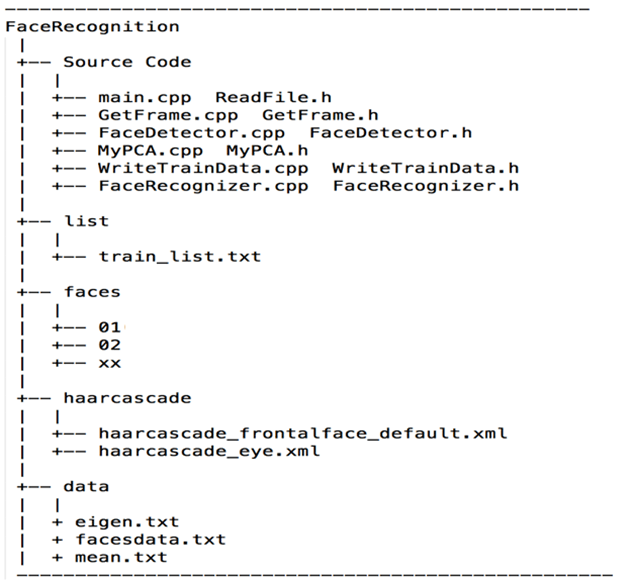
There are 5 classes in code:
- GetFrame: Capture frame from webcam
- FaceDetector: Detect face and eyes using Viola&Jones algorithm from OpenCV and crop face images to size 100x100
- MyPCA: The full PCA process, to get eigenvectors and eigenfaces
- WriteTrainData: Write training data that got in MyPCA to text file
- FaceRecognizer: Recognise input face from database
